I det här blogginlägget tänkte jag att vi skulle fördjupa oss lite i ett av de allra vanligaste sambanden som används i gymnasiets matematik nämligen Pythagoras sats. Det är ju aldrig fel att känna till lite kring historien, användningsområden, bevis och lite kuriosa kring de matematiska samband som du kanske dagligen jobbar med i din matematikkurs.
Pythagoras – Om den grekiska filosofen och matematikern
![pythagoras]() Pythagoras föddes år 580 f.v.t på ön Samos i nuvarande grekland. Inspirerad av bland annat matematikern Thales reste han till Egypten för att studera matematik och filosofi. När den persiske kungen invaderade Egypten fördes han till Babylonien som krigsfånge där han studerade deras filosofi och läror.
Pythagoras föddes år 580 f.v.t på ön Samos i nuvarande grekland. Inspirerad av bland annat matematikern Thales reste han till Egypten för att studera matematik och filosofi. När den persiske kungen invaderade Egypten fördes han till Babylonien som krigsfånge där han studerade deras filosofi och läror.
Efter ett tag återvände han till Samos men reste sedan vidare till Kronos i Italien där han grundade sitt sällskap pythagoréerna. Pythagoras och pythagoréerna trodd
e att världen var uppbyggd av heltal, läs mer om tal här, då även bråktal (rationella tal) kunde byggas upp med heltal. Enligt en legend lyckades en av hans lärjungar visa att $\sqrt{2}$ inte kunde skrivas som ett bråk då det är irrationellt och denne lärjunge skall för detta ha blivit belönad med döden genom dränkning!
Det som Pythagoras är allra mest känd för är dock den matematiska satsen som blivit döpt efter hans namn. Det är dock inte säkert att det är han som formulerade den först då den kan ha varit känd tidigare.
Vad säger pythagoras sats?
Pythagoras sats är intressant i gymnasiets matematik då den är en av de samband som återkommer i många olika områden. Det är inte bara sambandet i själv som du lär dig om i matematik 1 utan det återkommer i områden som trigonometriska triangelsatser, trigonometriska formler, komplexa talplanet, vektorer och talteori.
Innan vi nämner några typiska sådana användningsområden så kan vi först gå igenom vad denna sats egentligen säger.
Pythagoras sats
![pythagoras-sats-bild]()
I en rätvinklig triangel gäller att Hypotenusan i kvadrat är lika med med summan av kateterna i kvadrat.
Dvs att
$ a^2+b^2=c^2 $.
Pythagoras i gymnasiets matematik
Avstånd mellan punkter (i planet) och längden på vektorer
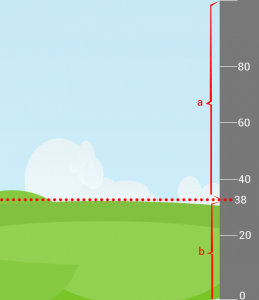
När man skall beräkna avstånd mellan två punkter kan Pythagoras sats användas till detta. Här används att det ofta är enklare att läsa av avståndet horisontellt eller lodrät mellan två punkter alternativt att man faktiskt känner till koordinaterna. Sedan kan de bägge punkterna bindas samman i en rätvinklig triangel och pythagoras sats kan användas för att bestämma avståndet.
Ovan nämnda metod kan generaliseras i avståndsformeln som säger att avståndet mellan två punkter $(x_1,y_1)$ och $(x_2,y_2)$ är
$d=\sqrt{(x_2-x_1)^2+(y_2-y_1)^2}$
Trigonometriska ettan
Pythagoras sats kan även användas för att ta fram olika samband inom trigonometrin. Ett exempel på ett sådant är trigonometriska ettan som säger att
$sin^2v+cos^2v=1$
Här använder man enhetscirkeln för att härleda detta samband. En förutsättning är att på enhetscirkeln är radien $1 \, l.e$.
![pythagoras-enhetscirkeln]()
Här gäller att vi punkten med x-värdet $cosv$ och y-värdet $sinv$ och vi ställer upp sambandet
$cos^2v+sin^2v=1^2 ⇔ $
$cos^2v+sin^2v=1 $
Här ovan har du sett två stycken områden där Pythagoras sats används i olika områden i gymnasiets matematik. Självklart finns det mer områden där detta samband kommer till användning, inte minst i olika problemuppgifter där sambandet kan vara en del av lösningen.
Ett enkelt gif bilds bevis för pythagoras (det finns över 100 till)
Det finns hundratals bevis för att Pythagoras sats verkligen stämmer, här samlas exempelvis 102 av dessa bevis.
Ett lite enklare visuellt bevis visas nedan i animationen.
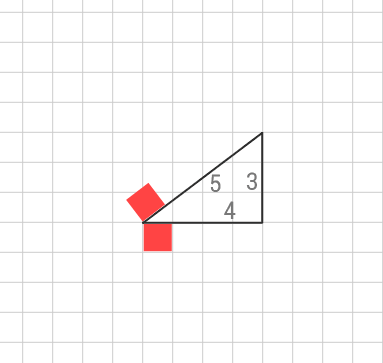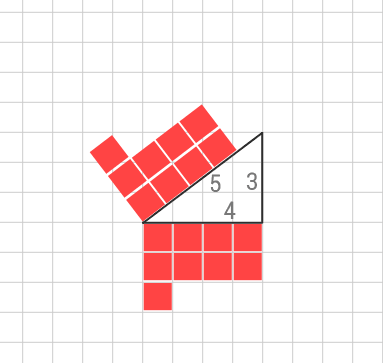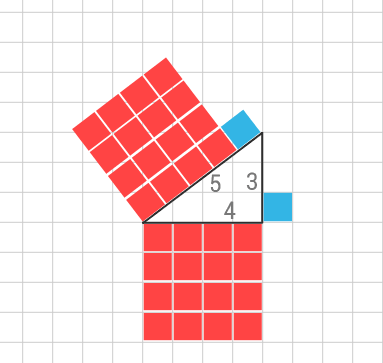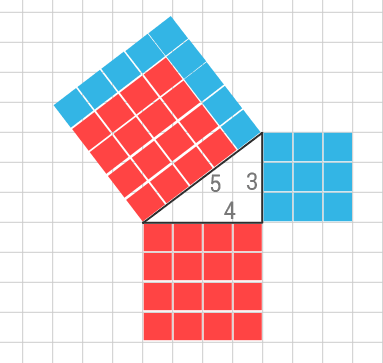
![pythagoras-sats-bevis]()
Här är en rätvinklig triangel som har kateterna 4 och 3 och hypotenusan 5 där pythagoras ger att $ 3^2+4^2=5^2 $. I bilden visas hur kvadraterna av kateterna ritas (16 respektive 9 stycken) samtidigt som kvadraten av hypotenusan (16+9=25) ritas ut. Här ser vi att summan av kateternas kvadrater är lika med hypotenusans kvadrat. Vi kan om vi vill byta ut 3:an, 4:an eller 5:an mot andra värden i en rätvinklig triangel och det går då att rita upp samma typ av bevis för denna.
Pythagoreiska tripplar
Jag tänkte att vi skulle avsluta det här blogginlägget med lite kuriosa kring några speciella rätvinkliga trianglar.
En typ av rätvinkliga trianglar som har fascinerat matematiker genom åren är de som kallas för pythagoreiska tripplar. En pythagoreisk trippel är en rätvinklig triangel som består av sidorna $a,\,b\,och\,c$ och där a, b, c är heltal sådan att
$ a^2+b^2=c^2 $
Exempel på sådana är
(3, 4, 5 )
(5, 12, 13)
(8, 15, 17)
(7, 24, 25)
Kan du hitta fler sådana här typer av trianglar?
The post Pythagoras sats – Ett samband som återkommer genom hela gymnasiet appeared first on Matematikvideo.














 Kanske drömmer du om att forska på det område som du tycker är allra mest intressant i framtiden?
Kanske drömmer du om att forska på det område som du tycker är allra mest intressant i framtiden?


