Ett område som var nytt i matematikkurserna på gymnasiet när Gy11 introducerades var det som handlar om vektorer. Tidigare har gymnasieelever framförallt läst och lärt sig om vektorer i samband med fysikkurserna men numera ingår alltså vektorer även för de elever som läser kurserna Matematik 1c och Matematik 2a. I det här blogginlägget tänkte jag att vi skulle gå igenom grunderna för att förstå en vektor och hur du även kan räkna med vektorer.
Vad är egentligen en vektor?

Om du skall förstå vad en vektor är för något så kan det vara bra att utgå från en verklig situation. Låt säga att din bil har slut på soppa och du måste be om hjälp att bli bogserad till närmsta bensinstation. Den bil som då har kopplat i bogserlinan i sin bil och därmed drar din bil kommer därmed att dra dig. I det här exemplet skulle vi kunna tänka oss att den kraft och riktning som bilen drar dig med kan visualiseras som en pil (en vektor). Den pil har både en riktning (det håll som bogserbilen drar åt) och en kraft (hur snabbt bogserbilen kör.)
En vektor beskriver alltså en storhet som både har en riktning och en storlek. Om du jämför detta med exempelvis storheter som längd eller vikt så har dessa endast en storlek.
Med hjälp av vektorer kan man beskriva en rad olika typer av storheter som kraft, acceleration eller magnetfält. Det handlar alltså om storheter som både har riktning och kraft.
Beteckning och symboler för vektorer
När man skall beteckna en vektor inom matematiken kan detta göras på lite olika vis. Det vanligaste sättet är att rita ut en pil ovanför den bokstav som betecknar vektorn. Det kan då se ut enligt
- $ \vec{v} $ – Vektorn v
- $ \vec{AB} $ – Vektorn med startpunkten A och slutpunkten B.
Ett annat sätt att beteckna vektorer kan vara att markera vektorn a i fet stil. I det här inlägget kommer vi att använda oss av en pil ovanför bokstaven/bokstäverna.
Rita ut en vektor
Det är mycket vanligt att man beskriver vektorer genom att rita ut dem som vektorpilar. Dels så är det ett bra sätt att förstå och räkna med vektorer men eftersom en vektor är en storhet med både kraft och riktning så är det också helt naturligt att visualisera dem genom att rita ut dem.
I bilden nedan är vektorn $ \vec{AB} $ utritad. I det här fallet har vi startpunkten A och slutpunkten B för vektorn. Startpunkten A har koordinaterna (1, 2) och slutpunkten B har koordinaterna (4, 4). I bilden är även en annan vektor utritad (den gröna). Det här är faktiskt samma vektor som $ \vec{AB} $ då den har samma storlek och riktning men här är startpunken flyttad till origo (0, 0). Då kan man även beskriva denna vektor endast med dess slutkoordinater (3, 2).
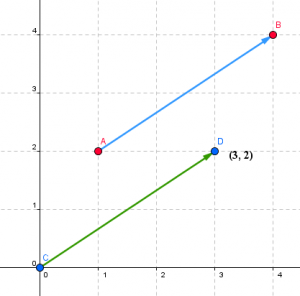
Det här gör alltså att även vektorn $ \vec{AB} = (3, 2) $.
Addera vektorer
När man adderar eller subtraherar vektorer kan detta göras både genom använda räknelagarna för detta om man känner till koordinaterna eller genom att använda visuella metoder som parallellogrammetoden eller polygonmetoden. När man adderar två vektorer så kallas summan för resultant. D.v.s. om vi adderar $ \vec{u} + \vec{v} = \vec{z} $ så kallas $ \vec{z} $ för resultant.
Parallellogrammetoden
Med hjälp av den här metoden kan du beräkna resultanten och samtidigt rita ut denna. Här gör du så att du ritar ut vektorerna så att de utgår ifrån samma punkte och skapar en parallellogram där diagonalen blir resultanten för additionen mellan de bägge vektorerna.
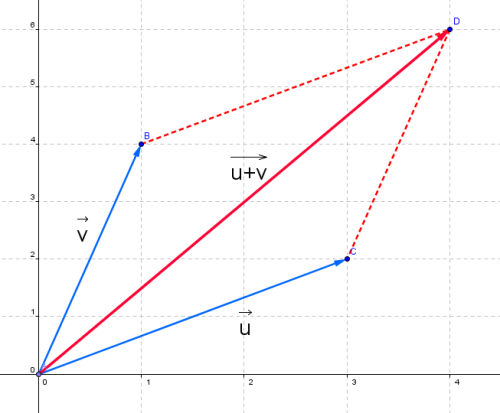
I bilden ser du hur vektorerna $ \vec{v} $ och $ \vec{u} $ adderas och får resultanten $ \vec{u+v} $
Polygonmetoden
Med polygonmetoden så gör du istället så att du flyttar vektorerna så att de är i följd. Resultanten blir då den vektor som har startpunkten i början av följden och slutpunkten i slutet på följden.
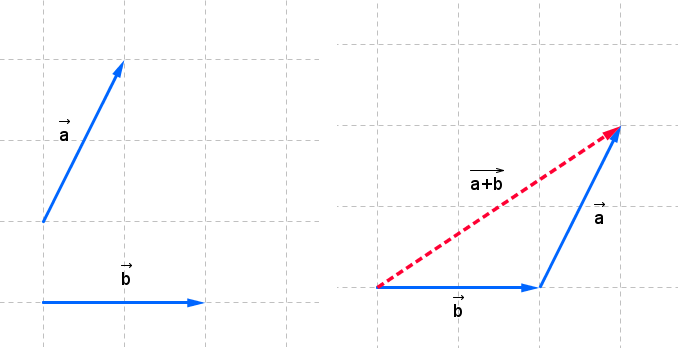
I bilden ovan ser du hur vektorn $ \vec{a} $ flyttas till slutet på vektorn $ \vec{b} $ så att vi kan rita ut resultanten $ \vec{a+b} $. Den här metoden är snabbare att utföra än parallellogrammetoden om du skall addera flera vektorer än två stycken.
Räknelagar för addition och subtraktion
Om man känner till koordinaterna för vektorerna så är det enkelt att addera eller subtrahera vektorer med hjälp av de räknelagar som finns. Om vi har vektorerna $ \vec{A} = (x_1, y_1) $ och $ \vec{B} = (x_2, y_2) $ så gäller att
- $ (x_1, y_1) + (x_2, y_2) = (x_1+x_2, y_1+y_2) $
- $ (x_1, y_1) – (x_2, y_2) = (x_1-x_2, y_1-y_2) $
Längden för en vektor $ \vec{u} $, med koordinaterna (a, b), brukar betecknas med $ | \vec{u} | $ och beräknas enligt
- $ | \vec{u} | = \sqrt{a^2 + b^2} $
